分享：基于Thermo-Calc和微观偏析统一模型对Al-6.32Cu-25.13Mg合金凝固路径的预测

闫二虎1, 2, , 孙立贤1, 徐芬1, 徐达鸣2

1 桂林电子科技大学材料科学与工程学院, 桂林 541004
2 哈尔滨工业大学材料科学与工程学院, 哈尔滨 150001

摘要

关键词： Al-Cu-Mg三元共晶合金 ; 凝固路径 ; 微观偏析统一模型 ; Thermo-Calc

合金凝固路径一般指在凝固过程中液相溶质浓度随温度的变化规律, 是多元多相合金固/液界面形态[1]和微观偏析[2]研究中经常遇到的问题. 二元合金凝固路径的模拟计算相对简单, 因为凝固路径会沿着相图中的液/固相线严格变化, 计算所需的一些参数可直接从相图中获得, 如相变温度和相变成分等[3]. 然而, 工业生产和研究实践中所用金属材料绝大多数为三元甚至多元合金, 即使是二元合金, 由于存在某些杂质元素, 尤其是当发生偏析导致杂质元素在某些局部地方富集时, 也应该将其作为多元合金来讨论[4,5]. 此外, 三元以及多元合金凝固组织中, 相种类繁多, 并且在不同凝固参数下同一成分的合金常以不同的凝固路径进行凝固, 使凝固路径的获取及后期分析存在一定的困难. 虽然可借助二元合金相图来近似处理, 但上述结果仅仅是对多元合金凝固路径的一个粗略近似. 因此, 对凝固过程中三元甚至多元合金的微观偏析模型化, 进而利用模拟计算方法预测其凝固路径是十分必要的.

目前, 凝固路径模拟计算的最佳途径是建立微观偏析模型并结合CALPHAD (calculation of phase diagram)计算相图[6,7]. 人们最早提出并且在许多凝固路径模拟计算中仍在广泛应用的微观偏析模型是Scheil模型与平衡杠杆定律(lever-rule), 因为上述模型不仅函数形式简单, 而且还分别真实地描述了2种极端条件下(DS=0和DS→∞; DS为固相中溶质扩散系数)的凝固溶质再分布行为[8-13]. 然而, 合金在实际凝固过程中, 需要考虑垂直穿过动态变化的复杂固/液界面的溶质扩散流矢量, 因此上述模型并不适用[14]. Flemings和Brody[15]首次提出了一种考虑弱固相反扩散 (solid back diffusion, SBD)下的溶质再分布模型. Clyne和Kurz[16]扩展了上述模型的应用范围, 并首次统一了任意SBD效应. 然而, 上述模型均按一维空间建立, 且将凝固中的枝晶形态简化为“板状”, 造成凝固后期合金的凝固路径模拟计算结果与实际情况相差甚远, 因此, 在模型建立过程中应将不同的枝晶形态考虑进来. 为解决该问题, Ohnaka[17]在模型建立过程中将枝晶形态简化为2种基本形态: “板状”和“圆柱状”, 而后Kobayashi[18]对含有上述枝晶形态的溶质扩散方程进行了严格的解析求解, 首次得出了任意SBD下溶质再分布的精确解析表达式. Nastac和Stefanescu[19]对“球状、圆柱状与板状”凝固过程固相与液相中的溶质扩散方程进行了联立解析求解, 得到含有这3种几何单元体固相与液相中溶质再分布的统一表达式. 随着上述微观偏析模型的改进, 三元及多元合金凝固路径的预测取得了较大进展.

在预测合金凝固路径时, 虽然微观偏析模型占据了举足轻重的位置, 但如何通过CALPHAD计算相图(如Thermo-Calc软件)来获取凝固热力学数据也是十分重要的. Larouche[20]通过Thermo-Calc软件及质量守恒方程来获取热力学数据, 进而对多元多相合金凝固路径进行了成功的预测. Du等[21]提出了二维多元合金微观偏析模型, 并将该模型与“准界面跟踪模型”相结合, 同时耦合Thermo-Calc软件的热力学数据库, 研究了三元铝合金的枝晶生长及其凝固路径. Hao等[22]用Thermo-Calc软件结合实验研究, 对一系列的Al, Ni等多元合金体系进行了热力学优化与相图计算研究, 为合金凝固路径模拟计算提供了大量可靠的热力学数据. 陈福义和介万奇[23]通过Thermo-Calc软件获取的热力学数据, 成功地对Al-Cu-Zn合金的凝固路径进行了预测. 在本课题组前期工作[24]中, 将二元合金凝固传输模型及算法扩展到多元合金, 并提出了耦合Thermo-Calc计算多元合金“温度-固相体积分数-液相成分” 3者之间的数值算法. 其中, 耦合Thermo-Calc获取热力学参数时使用到以下3种方法: 直接耦合计算法、查表法和拟合函数法. 上述研究结果表明, 通过Thermo-Calc软件获取热力学参数进行相图热力学计算是一种通用可行的方法.

Al-Cu, Al-Mg和Cu-Mg二元合金应用广泛、具有广阔的应用前景, 已引起了众多研究学者的兴趣, 而以此为基础的Al-Cu-Mg合金研究一般仅局限于富Al角位置(图1中方框区域), 高Mg含量的Al-Cu-Mg合金研究鲜有报道. 本课题组前期工作[13,24]虽然基于微观偏析统一模型并耦合Thermo-Calc软件对Al-Cu-Si, Al-Cu-Mg和Al-Si-Mg等三元合金系凝固路径成功进行了数值计算, 但对于Mg含量较高的Al-Cu-Mg合金的凝固路径及微观偏析行为还没有研究. 基于此, 本工作首先研究了不同冷却速率以及不同固相反扩散系数Φ (Φ=0: Scheil模型; Φ=1: Level-rule模型)对Al-6.32Cu-25.13Mg合金凝固路径的影响; 而后计算了上述各条件下显微组织中的初生相体积分数、两相共晶体积分数和三相共晶体积分数; 最后, 通过不同冷却速率下的实验对上述模拟计算结果进行了比较和验证.

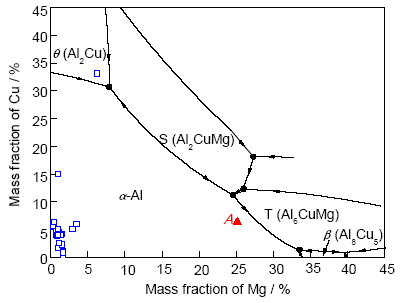
图1   Al-Cu-Mg三元合金相图[25]及Al-6.32Cu-25.13Mg合金在相图中的位置

Fig.1   Phase diagram of the Al-Cu-Mg ternary alloy system[25] and the position of Al-6.32Cu-25.13Mg ternary alloy on the phase diagram which has been marked as A (The box areas represent the previous studies)

1 数值模型

图1给出了Al-Cu-Mg三元合金相图[25]以及Al-6.32Cu-25.13Mg合金位于相图中的位置(A点). 可见, 该成分点位于α-Al固溶体相区, 在平衡凝固条件下, 该合金可能会经历3种凝固过程: 单相凝固(L→α), 两相共晶凝固(L→α+T)及后期在447.9 ℃发生的三相共晶凝固(L→α+β+T). 因此, 本工作在数值模型的建立过程中包含了上述3种情况.

1.1 数值模型

图2给出了合金凝固过程中的模型示意图, 并做出如下假设: (1) 合金凝固过程中无气泡生成; (2) 枝晶动态生长的固/液(S/L)界面处时刻保持热力学平衡; (3) 二元共晶整体作为一相围绕初生相长大; (4) 在整个凝固过程中fS+fL=1 (fS和fL分别代表固相和液相体积分数); (5) 液态流动符合Newton流体层流. 基于上述假设, 多元合金凝固过程中微元体内的混合介质平均成分项ρCn可以表述为[26,27]:

$\begin{array}{c}\partial (\rho C_n{)}_m/\partial t=({\rho }_S{C}_{\mathit{nS}}{)}^{*}\partial f_S/\partial t+{\int }_0^{f_S}\left[\partial \right({\rho }_S{C}_{\mathit{nS}}\raisebox{1ex}{$)$}\!\left/ \!\raisebox{-1ex}{$\partial $}\right.t]\mathit{d\eta }+\end{array}$$\begin{array}{c}\mathit{}\left({\rho }_L{C}_{\mathit{nL}}\right)\partial f_L/\partial t+f_L\partial ({\rho }_L{C}_{\mathit{nL}}\raisebox{1ex}{$)$}\!\left/ \!\raisebox{-1ex}{$\partial $}\right.t\end{array}$(1)

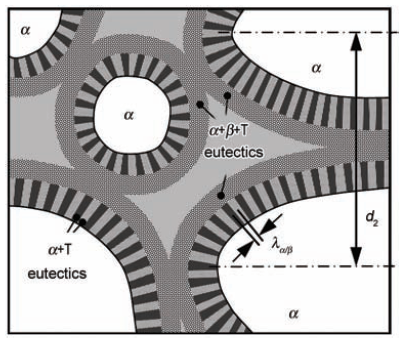
图2   微观偏析数值模型示意图

Fig.2   Schematic growth of α-dendrites and binary eutectic (α+β) in a ternary solidification system (ternary eutectic (α+β+T) may form from a part of the interdendritic liquid (L-phase) in a later solidification stage, λ represents the space between α and β phases and d2 represents the space between primary α phases)

式中, CnL和CnS (n=1, 2)分别表示液相和固相中组元n的浓度, $\begin{array}{c}{\rho }_L\end{array}$和 $\begin{array}{c}{\rho }_S\end{array}$分别表示液相和固相的密度, t为凝固时间, η为凝固枝晶中等浓度线对应的体积分数, m代表在固/液两相区任意一点处取的微单元, *为微单元内固/液界面处. 对式(1)右端积分项的求解, 需掌握枝晶凝固过程中的精确信息, 而在实际凝固过程当中, 枝晶的形态异常复杂, 千变万化, 故从实际的凝固过程中去捕捉枝晶的复杂形态以及跟踪其变化这一方法是不可取的. 本课题组前期的工作[26-29]曾将“几何权重平均技术”引入, 用来描述凝固过程中时刻变化的枝晶形态, 从而成功求解了式(1)中的右端积分项, 最终简化整理得:

$\begin{array}{c}\partial (\rho C_n{)}_m/\partial t=({\rho }_S{C}_{\mathit{nS}}{)}^{*}\partial f_S/\partial t+\Phi f_S\partial ({\rho }_S{C}_{\mathit{nS}}{)}^{*}/\partial t+\end{array}$

$\begin{array}{c}\mathit{}\left({\rho }_L{C}_{\mathit{nL}}\right)\partial f_L/\partial t+f_L\partial ({\rho }_L{C}_{\mathit{nL}}\raisebox{1ex}{$)$}\!\left/ \!\raisebox{-1ex}{$\partial $}\right.t\end{array}$(2)

式中, Φ为固相反扩散系数, 取值范围为0~1, 两端取值分别与Scheil模型和Lever-rule模型相互对应. 将式(1)和(2)置于一个封闭的微元体内时, 上述混合介质平均成分项恒为零, 也就是说微元体内不进行任何的溶质元素交换, 即: $\begin{array}{c}\partial (\rho C_n{)}_m/\partial t=0\end{array}$, 于是得出:

$\begin{array}{c}({\rho }_S{C}_{\mathit{nS}}{)}^{*}\partial f_S/\partial t+\Phi f_S\partial ({\rho }_S{C}_{\mathit{nS}}{)}^{*}/\partial t+\end{array}$

$\begin{array}{c}\left({\rho }_L{C}_{\mathit{nL}}\right)\partial f_L/\partial t+f_L\partial ({\rho }_L{C}_{\mathit{nL}}\raisebox{1ex}{$)$}\!\left/ \!\raisebox{-1ex}{$\partial $}\right.t=0\end{array}$(3)

假定溶质分配系数k, $\begin{array}{c}{\rho }_S\end{array}$, $\begin{array}{c}{\rho }_L\end{array}$以及凝固收缩系数 $\begin{array}{c}\beta ={\rho }_S/{\rho }_L-1\end{array}$均保持恒定值, 将固/液界面处的固相浓度 $\begin{array}{c}{C}_S^{*}=k{C}_L^{*}\end{array}$和 $\begin{array}{c}{f}_L=1-f_S\end{array}$代入式(3), 并考虑到液相浓度最初值 $\begin{array}{c}{C}_{L,f_S=0}=C_0\end{array}$, 整理化简得出下式(4)[28]:

$\begin{array}{c}\partial C_{\mathit{nL}}/\partial t=[1-(1+\beta \left)k\right]C_{\mathit{nL}}/\{1-[1-(1+\beta )\mathit{k\Phi }\left]f_S\right\}\end{array}$(4)

当忽略了凝固收缩率的影响, 即令β=0, 此时式(4)整理简化为:

$\begin{array}{c}{C}_{\mathit{nL}}=C_{n0}[1-(1-\mathit{\Phi k})f_S{]}^{(k-1)/(1-\mathit{\Phi k})}\end{array}$(5)

式中, Cn0 (n=1, 2)分别表示原始合金中组元n的浓度. Φ表达式为:

$\begin{array}{c}\Phi =\mathit{\theta \phi }/(1+\mathit{\theta \phi })\end{array}$(6)

式中, 无量纲参数θ代表枝晶间液相成分对SBD效应的敏感性参数:

$\begin{array}{c}\theta =(1+\beta )k{f}_S/f_L^2\end{array}$(7)

无量纲参数φ代表枝晶几何形貌修正的溶质扩散Fourier因子. 推导过程和公式中相关参数定义和取值详见文献[28]和[29]. 从式(5)~(7)的推导过程可看出, 本工作数值模型不仅可以统一地表达包括Scheil与Lever-rule模型极限溶质再分布在内的任意SBD效应, 以及其它有关合金物性参数的影响, 而且还包含了任意凝固枝晶几何形貌等因素.

1.2 数值算法

本工作凝固路径算法首先需要搭建TQ 6.0接口程序, 而后在源代码基础上与Thermo-Calc软件进行耦合, 用以获取凝固热力学数据, 如相名称及其个数、相结晶温度及溶质分配系数等. 在每一步的迭代计算中, 平衡相的数量和种类均与上一步计算结果相比较, 用以判定合金进入到哪种凝固阶段. 初生相及两相共晶凝固阶段的迭代计算以fS作为控制变量, 采用“不动点迭代法”来进行数值求解. 三相共晶凝固阶段的迭代计算以温度梯度ΔT作为控制变量. 各凝固阶段的溶质成分Cu通过Thermo-Calc来获取, 溶质成分Mg通过微观偏析统一模型迭代计算得出, 直至凝固终止, 凝固路径计算的详细算法见文献[30].

2 实验过程

Al-7Cu-25Mg (质量分数, %, 下同)三元合金(实测成分为Al-6.32Cu-25.13Mg)由高纯Al (99.99%), Mg (99.99%)及Al-54.2Cu中间合金在CO2和SF6 (体积比为40∶1)保护气下采用井式电阻炉熔炼的方法配制而成. 实验过程中, 首先将熔融的金属液(840~850 ℃)同时浇注到石墨型、水玻璃砂型、Al2SiO5纤维毡保温棉型和恒温型4种铸型中, 并使用十六通道数据采集系统(XJY-160)采集各铸型温度数据, 直至合金液凝固完毕, 用来获取不同的凝固冷却速率. 经测定, 4种铸型中的冷却速率分别为0.1, 0.06, 0.005和0.0007 ℃/s. 实验结束后, 在试样中心部位取样, 并经清洗、打磨、抛光后制备成所需样品. 采用带有能谱(EDS)分析仪的JSM-6480型扫描电镜(SEM)对其进行显微组织观察, 并对观察到的各相进行EDS分析. 最后, 利用Image-Pro Plus软件对凝固组织中的各相进行测量.

3 实验结果与讨论

3.1 不同冷却速率下的凝固路径

三元合金凝固路径的影响因素很多, 如: 冷却速率、固相反扩散系数、枝晶粗化、过冷度等[31,32]. 本工作首先计算了4种不同冷却速率下(Rf=0.1, 0.06, 0.005, 0.0007 ℃/s) Al-6.32Cu-25.13Mg合金的凝固路径, 如图3所示, 计算中所用的合金物性参数如表1所示.

图3   不同冷却速率下Al-6.32Cu-25.13Mg合金凝固路径的计算结果

Fig.3   Calculated results for Al-6.32Cu-25.13Mg alloy with different solidification rates Rf

从图3可以看出, 该合金在4种不同冷却速率下的凝固过程均经历了单向凝固L→α, 两相共晶凝固L→α+T和三相共晶凝固L→α+β+T 3个凝固阶段, 说明冷却速率对合金的凝固路径基本没有影响, 也就是说, 当冷却速率较大时, 该合金凝固时依然会经历上述3个凝固阶段. 然而, 冷却速率对凝固组织中各相体积分数的影响较大, 如图3b所示, 随着冷却速率的逐渐降低, 显微组织中初生相体积分数Vα基本不变, 两相共晶体积分数V2E增多而三相共晶体积分数V3E减少. 这主要是因为逐渐降低的冷却速率使得参与后期三元共晶转变的残余合金液体越来越少, 进而造成了三相共晶体积分数的降低.

图4为凝固组织中两相共晶体积分数和三相共晶体积分数随凝固速率的变化曲线. 可以看出, 随着冷却速率的降低, V2E由67%增加到75%, 而V3E由原来的20%下降为11%. 结合线性回归分析得出上述三者之间的拟合关系为: V2E=-2.5lgRf+64.9; V3E=2.5lgRf+22.12.

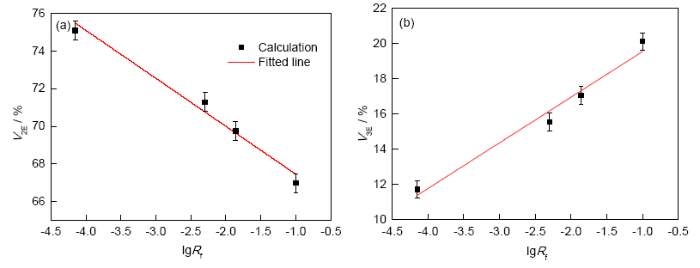
图4   两相共晶组织体积分数和三相共晶组织体积分数与凝固速率关系曲线

Fig.4   Fitted curves of volume fraction of binary eutectic V2E (a) and ternary eutectic V3E (b) vs Rf

3.2 不同固相反扩散系数下的凝固路径

从式(1)~(4)的推导过程中可看出, 本工作微观偏析统一模型可分别简化为严格的Scheil模型(即DS=0)与Lever-rule模型(DS→∞). 事实上, 上述2个模型和本工作模型均具有统一的简单指数函数形式, 即微观溶质再分布的一般式(5), 不同的只是模型中参数Φ的表达式及取值不同. 当Φ由0逐渐向1过渡时, 暗示着合金凝固时固相反扩散程度变大, 进而影响合金的凝固结晶以及最终的凝固路径. 基于此, 本工作对不同固相反扩散系数(Φ=0, 1/3, 2/3, 5/6, 1)下的Al-6.32Cu-25.13Mg合金凝固路径进行了计算, 如图5所示. 可以看出, 固相反扩散系数的变化对Al-4.37Cu-27.02Mg合金凝固路径影响较大, 当Φ处于0~5/6之间时, 合金凝固时经历以下3个阶段: 单向凝固(L→α), 两相共晶凝固(L→α+T)和三相共晶凝固(L→α+β+T); 当Φ处于5/6~1之间时, 合金凝固时仅经历前2个凝固阶段, 即: 单向凝固(L→α)和两相共晶凝固(L→α+T). 此外, 随着固相反扩散系数的增加, 显微组织中初生相和两相共晶体积分数变大, 而三相共晶体积分数变小直至为0.

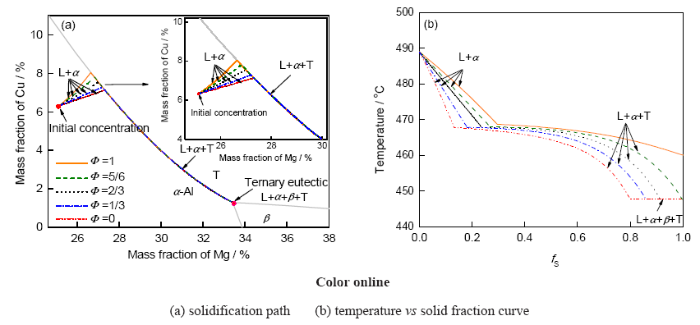
图5   不同固相反扩散系数Φ下Al-6.32Cu-25.13Mg合金凝固路径的计算结果

Fig.5   Calculated results for Al-6.32Cu-25.13Mg alloy with different solid back diffusion coefficients Φ

为解释上述现象, 图6给出了不同固相反扩散系数下的CL-fS变化曲线. 可以看出, 合金凝固自始至终, 溶质原子在结晶固相与液相之间均存在复杂的传输和扩散. 液相中的溶质Cu原子含量随着α相的析出而增加, 而后伴随着两相共晶的凝固而降低; 而溶质Mg原子含量随液相中α相和两相共晶的析出而持续增加, 最后溶质原子在三相共晶凝固阶段趋于平衡. 在初生α相析出阶段, 溶质Cu和Mg原子含量随着Φ的增加均减少, 当Φ=1时, 即凝固过程中充分固相反扩散(DS→∞), 初生α相的生长需要周围液相中可供固相生长的溶质原子, 进而使得固/液界面处溶质原子平均值要低于非平衡凝固时的平均值; 在两相共晶凝固阶段, 随着Φ增加, 液相中的Cu原子含量逐渐增加而Mg原子含量逐渐降低, 这是由于两相共晶在生长过程中需要固/液界面处供给更多的Mg原子和较少的Cu原子, 进而造成了液相中Mg原子的缺失和Cu原子的富集. 由于Φ=1时已凝固的两相共晶中存在充分的固相反扩散, 溶质原子间的互补使得两相共晶快速生长, 直至凝固结束; 最后, 在三相共晶凝固阶段, Mg和Cu原子含量维持恒定不变.

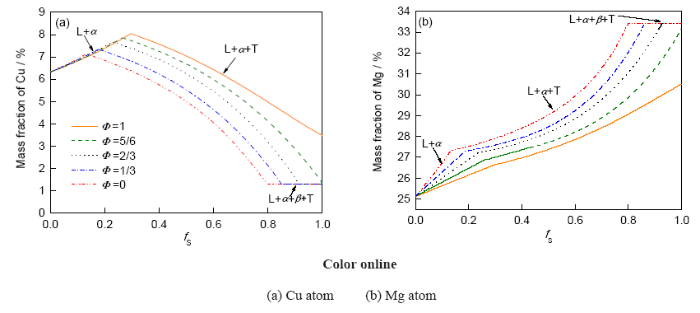
图6   Al-6.32Cu-25.13Mg三元合金凝固过程中CL-fS曲线

Fig.6   Comparison of CL-fS curves for Al-6.32Cu-25.13Mg alloy with different Φ

3.3 不同冷却速率下的显微组织

图7给出了Al-6.32Cu-25.13Mg合金在4种不同铸型中的凝固冷却曲线. 可以看出, 每条曲线上均出现了3个平台, 分别代表了初生α相、两相共晶(α+T)和三相共晶(α+T+β)的析出. 三元共晶反应温度为450.09 ℃, 比Thermo-Calc计算的平衡凝固结晶温度高3 ℃.

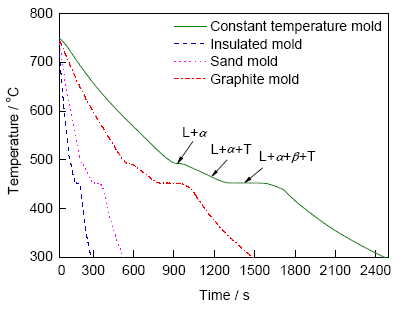
图7   Al-6.32Cu-25.13Mg三元合金在4种不同铸型中的凝固冷却曲线

Fig.7   Cooling curves of the Al-6.32Cu-25.13Mg alloy in different molds

为确定凝固过程中是否有新相生成, 对不同冷却速率下的凝固试样进行了显微组织观察, 并对各相进行EDS分析, 如图8所示. 结果表明, 在黑色相、深灰色相和浅灰色相中, Al, Cu和Mg原子百分比分别为XAl∶XCu∶XMg=86.3∶0.79∶12.91, 62.78∶1.69∶35.53和55.53∶9.1∶35.57, 说明黑色相为α-Al相, 深灰色相为β (Al8Mg5)相, 浅灰色相为T (Al6CuMg4)相, 如图8a所示. 从图8还可以看出, 4种冷却速率下, Al-6.32Cu-25.13Mg合金显微组织中均存在初生α相、两相共晶(α+T)和三相共晶(α+T+β), 说明在4种冷却速率下合金的凝固路径均为: 初生相(L→α)析出、两相共晶(L→α+T)反应和三相共晶(L→α+T+β)反应, 与图3中的模拟计算结果吻合. 此外, 从图8中还可以看出, 初生α相呈等轴枝晶形态, 两相共晶依附在初生相周围并呈现出“层状”和“棒状”形态, 三相共晶呈“离异共晶”形态分布在两相共晶周围. 随着冷却速率逐渐降低, 两相共晶体积分数逐渐增加而三相共晶体积分数逐渐减少.

图8   Al-6.32Cu-25.13Mg合金在4种冷却速率下显微组织的SEM像

Fig.8   SEM images of Al-6.32Cu-25.13Mg ternary alloy under cooling rates of 0.1 ℃/s (a), 0.06 ℃/s (b), 0.005 ℃/s (c) and 0.0007 ℃/s (d)

3.4 实验结果与模拟计算对比

采用Image-Pro Plus金相定量分析软件, 对4种不同冷却速率下凝固组织中初生相、两相共晶和三相共晶的体积分数进行了定量分析与测量, 并与模拟计算结果进行对比, 测量值与模拟计算值的汇总如表2所示.

从表2可以看出, 该合金在4种不同冷却速率下初生相、两相共晶和三相共晶的体积分数相差较小, 三者体积分数测量值与模拟计算值的最大差值分别为0.14%, 2.1%和-1.6%, 这主要是由于在微观偏析模型建立过程中忽略了形核过程以及孔洞形成等因素. 但值得注意的是, 在各冷却速率下, 初生相、两相共晶和三相共晶体积分数测量值与模拟计算值之和差值约为0, 说明合金整个凝固过程中的测量值与模拟计算值相互吻合. 此外, 随着冷却速率的降低, 两相共晶体积分数测量值逐渐增加, 三相共晶体积分数测量值逐渐降低, 与图3和4的模拟计算结果相互吻合.

4 结论

(1) 冷却速率Rf对Al-6.32Cu-25.13Mg合金的凝固路径影响较小, 当Rf处于0.1~0.0007 ℃/s范围时, 该合金的凝固路径均为: (L+α)→(L+α+T)→(L+α+β+T); 随着冷却速率的降低, 显微组织中初生相体积分数Vα基本不变, 两相共晶体积分数V2E增大而三相共晶体积分数V3E减少, 上述参数满足V2E=-2.5lgRf+64.9, V3E=2.5lgRf+22.12.

(2) 固相反扩散系数Φ对该合金的凝固路径影响较大, 当Φ由0逐渐增大至1时, 合金的凝固路径由(L+α)→(L+α+T)→(L+α+β+T)逐渐变为(L+α)→(L+α+T); Φ的增加使得显微组织中的Vα和V2E变大而V3E变小.

(3) Al-6.32Cu-25.13Mg合金凝固组织中仅包含α-Al, β (Al8Mg5)和T (Al6CuMg4)三相, 其中, 初生α相呈等轴枝晶态分布, 两相共晶(α+T)依附在初生α相周围并呈现出“层状”和“棒状”形态, 三相共晶(α+β+T)呈“离异共晶”形态分布在上述两相共晶周围.

(4) 通过对Al-6.32Cu-25.13Mg三元合金凝固路径的实验验证, 表明本工作微观偏析统一模型耦合Thermo-Calc软件对其凝固路径的预测是有效、可行的.